Answer:
The question is not complete.
I believe this is the correct complete question:
The following sample of six measurements was randomly selected from a normally distributed population: 1, 3, -1, 5, 1, 2.
a. Test the null hypothesis that the mean of the population is 3 against the alternative hypothesis,
μ<3 Use α=.05
b. Test the null hypothesis that the mean of the population is 3 against the alternative hypothesis,
μ≠3 Use α=.05
c. Find the observed significance level for each test.
Explanation:
We will first find the standard deviation (S.D) of the six measurements.
To find the S.D, we calculate the mean and variance
Mean = ∈n/n where ∈n = sum of set of numbers n
Mean = [1+3+(-1)+5+1+2] / 6 where n = 6
Mean = 11/6 = 1.8
Variance = Sum of squared deviation from mean / n-1
Variance = [(1-1.8)² + (3-1.8)² + (-1-1.8)² + (5-1.8)² + (1-1.8)² + (2-1.8)²] / 6-1
Variance = [0.64 + 1.44 + 7.84 + 10.24 + 0.64 + 0.04] / 5 = 20.84/5 = 4.168
Standard Deviation S.D = √Variance = √4.168 = 2.041
(a)
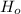: μ=3,
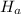: μ<3
Using α=0.05
test stat = {mean - μ
] / S.D /
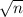= [1.8 - 3] / [2.041/ √6
test stat = -1.2 / 0.833 = -1.44
Critical Value from Student T distribution is t
= 2.015
Therefore, the rejection value contains values < -2.015
-1.400 > -2.015. It Fails to reject
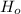
(b)
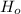: μ = 3,
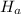: μ ≠ 3
Using α=0.05
test stat = {mean - μ
] / S.D /
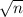= [1.8 - 3] / [2.041/ √6
test stat = -1.2 / 0.833 = -1.44
Critical Value from Student T distribution is t
= 2.571
Therefore, the rejection value contains values < -2.571 and larger value to 2.571
2.571 > -1.400 > -2.571. It Fails to reject
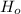
(c) Significance Value of (a) is P-value > 0.100
Significance Value of (b) is P-value > (2 x 0.100 = 0.200)