Question

`\frac{ {x}^(3) }{x { }^(2) + 2x + 1}`

Hi! I need help with the problem above. I know the answer to it is x-2+((3x+2)/(x^2+2x+1)), but I need help knowing and understanding the process. I can usually divide polynomials with ease, but I have never had to divide when the divisor is larger than the dividend. Can you please show me how to solve this with long division? Also, if you still have time to help me, how would synthetic division work with this? Thank you in advance!​

Answer 1

Since

`(x^3)/(x^2+2x+1)=(x^3)/((x+1)^2)`

we can perform synthetic division twice, first for

`(x^3)/(x+1)`

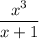
then dividing the result by
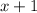`x+1` again.

... || 1 0 0 0

-1 || -1 1 -1

================

... || 1 -1 1 -1

This translates to

`(x^3)/(x+1)=x^2-x+1-\frac1{x+1}`

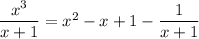
Now divide
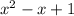`x^2-x+1` by
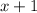`x+1`. (Dividing the remainder term by
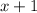`x+1` can wait until the end.)

... || 1 -1 1

-1 || -1 2

=============

... || 1 -2 3

or equivalently,

`(x^2-x+1)/(x+1)=x-2+\frac3{x+1}`

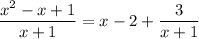
Taking everything together, we have

`(x^3)/(x^2+2x+1)=(x^2-x+1)/(x+1)-\frac1{(x+1)^2}`

`(x^3)/(x^2+2x+1)=x-2+\frac3{x+1}-\frac1{(x+1)^2}`

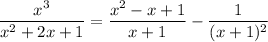
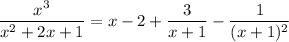
Combine the last two fractions:

`(x^3)/(x^2+2x+1)=x-2+(3(x+1)-1)/((x+1)^2)`

`(x^3)/(x^2+2x+1)=x-2+(3x+2)/((x+1)^2)`

which agrees with the solution we found in your other question.

(There's a variant of synthetic division that works with directly dividing a polynomial by another one of any degree, but it's basically just a condensed version of applying the algorithm for dividing a polynomial twice by a linear one, like we've done here.)