Answer:
The question is missing the values, I found a possible matching question:
a city has a population of 380,000 people. suppose that each year the population grows by 7.5%. what will be the population after 6 years
Answer:
After 6 years, the population will be 586, 455 people
Explanation:
This growth is similar to the growth of an invested amount of money, which is compounded annually, yielding a future value, when it increases by a certain interest rate. Hence the formula for compound interest is used to determine the population after 6 years as follows:
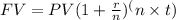
where
FV = future value = population after 6 years = ???
PV = present value = current population = 380,000 people
r = interest rate = growth rate = 7.5% = 7.5/100 = 0.075
n = number of compounding periods per year = annually = 1
t = time of growth = 6 years
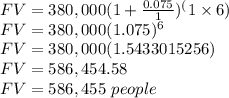
Therefore, after 6 years, the population will be 586, 455 people