Answer:
1. Yes, there is sufficient evidence to support the claim that men have a higher rate of red/green color blindness than women.
2. The 95% confidence interval for the difference between the color blindness rates of men and women is [0.0656, 0.1004].
Explanation:
We are given that in a study of red/green color blindness. 1000 men and 2800 women are randomly selected and tested
Among the men, 85 have red/green color blindness. Among the women, 6 have red/green color blindness.
Let
 = population proportion of men having red/green color blindness.
= population proportion of men having red/green color blindness.
 = population proportion of women having red/green color blindness.
= population proportion of women having red/green color blindness.
So, Null Hypothesis, : {means that men have a lesser or equal rate of red/green color blindness than women}
Alternate Hypothesis, : {means that men have a higher rate of red/green color blindness than women}
(1) The test statistics that will be used here is Two-sample z-test statistics for proportions;
T.S. = ~
N(0,1)
where, = sample proportion of men having red/green color blindness = = 0.085
 = sample proportion of women having red/green color blindness =
= sample proportion of women having red/green color blindness =
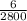 = 0.002
= 0.002
 = sample of men = 1000
= sample of men = 1000
 = sample of women = 2800
= sample of women = 2800
So, the test statistics =
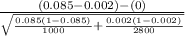
= 9.37
The value of z-test statistics is 9.37.
Also, the P-value of the test statistics is given by;
P-value = P(Z > 9.37) = Less than 0.0001
Since the P-value of our test statistics is less than the level of significance as 0.0001 < 0.05%, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region.
Therefore, we support the claim that men have a higher rate of red/green color blindness than women.
(2) The 95% confidence interval for the difference between the color blindness rates of men and women (
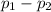 ) is given by;
) is given by;
95% C.I. for (
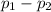 ) =
) =
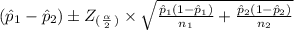
=
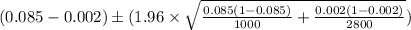
=

= [0.0656, 0.1004]
Here, the crtical value of z at 2.5% level of significance is 1.96.
Hence, the 95% confidence interval for the difference between the color blindness rates of men and women is [0.0656, 0.1004].