Question

Seven baseballs are randomly selected from the production line to see if their stitching is straight. Over time, the company has found that 89.4% of all their baseballs have straight stitching. If exactly five of the seven have straight stitching, should the company stop the production line

Answer 1

The probability that exactly five of the seven have straight stitching is very low only 13.47%, this means that the company should stop the production line.

Explanation:

We are given that Seven baseballs are randomly selected from the production line to see if their stitching is straight. Over time, the company has found that 89.4% of all their baseballs have straight stitching.

Let X = Number of baseballs having straight stitching

The above situation can be represented through the binomial distribution;

`P(X = r) = \binom{n}{r} * p^(r)* (1-p)^(n-r);x=0,1,2,3,.......`

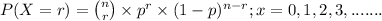
where, n = number of samples (trials) taken = 7 baseballs

r = number of success = exactly 5

p = probbaility of success which in our question is the probability

that baseballs have straight stitching, i.e.; p = 89.4%

So, X ~ Binom(n = 7, p = 0.894)

Now, the probability that exactly five of the seven have straight stitching is given by = P(X = 5)

P(X = 5) =
`\binom{7}{5} * 0.894^(5)* (1-0.894)^(7-5)`

=
`21 * 0.894^(5)* 0.106^(2)`

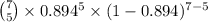
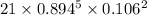
= 0.1347 or 13.47%

Since the probability that exactly five of the seven have straight stitching is very low only 13.47%, this means that company should stop the production line.