Question

A simple random sample of 36 men from a normally distributed population results in a standard deviation of 10.1 beats per minute. The normal range of pulse rates of adults is typically given as 60 to 100 beats per minute. If the range rule of thumb is applied to that normal​ range, the result is a standard deviation of 10 beats per minute. Use the sample results with a 0.10 significance level to test the claim that pulse rates of men have a standard deviation equal to 10 beats per minute.

Complete parts​ (a) through​ (c) below.
a. Identify the null and alternative hypotheses.
b. Compute the test statistic. χ2 = ___ (round to three decimals)
c. Find the​ P-value. ​P-value=____​(Round to four decimal places as​ needed.)
d. State the conclusion. (reject null/ eccept null)

Answer 1

Explanation:

Given that:

sample size n = 36

standard deviation = 10.1

level of significance ∝ = 0.10

The null hypothesis and the alternative hypothesis can be computed as follows:

`H_0 : \sigma = 10`

`H_1 : \sigma \\eq 10`

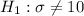
The test statistics can be computed as follows:

`X^2 = ((n -1)s^2 )/(\sigma ^2)`

`X^2 = ((36 -1)10.1^2 )/(10^2)`

`X^2 = ((35)102.01 )/(100)`

`X^2 = (3570.35 )/(100)`

`X^2 =35.704`

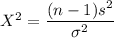
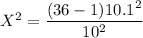
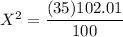
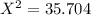
degree of freedom = n - 1 = 36 - 1 = 35

Since this test is two tailed .

The P -value can be determined by using the EXCEL FUNCTION ( = 2 × CHIDIST(35.7035, 35)

P - value = 2 × 0.435163515

P - value = 0.8703 ( to four decimal places)

Decision Rule : To reject the null hypothesis if P - value is less than the 0.10

Conclusion: We fail to reject null hypothesis ( accept null hypothesis) since p-value is greater than 0.10 and we conclude that there is sufficient claim that the normal range of pulse rates of adults given as 60 to 100 beats per minute resulted to a standard deviation of 10 beats per minute.