Question

The half-life of radium-226 is 1590 years. if a sample contains 100 mg, how many mg will remain after 1000 years?

Answer 1

`a=64.7mg`

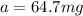
Step-by-step explanation:

Hello,

In this case, we need to remember that for the required time for a radioactive nuclide as radium-226 to decrease to one half its initial amount we are talking about its half-life. Furthermore, the amount of remaining radioactive material as a function of the half-lives is computed as follows:

`a=a_0((1)/(2) )^{(t)/(t_(1/2)) }`

Therefore, for an initial amount of 100 mg with a half-life of 1590 years, after 1000 years, we have:

`a=100mg((1)/(2) )^{(1000years)/(1590years) }\\\\a=64.7mg`

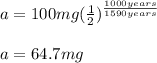
Best regards.