Question

The CEO of a large corporation asks his Human Resource (HR) director to study absenteeism among its executive-level managers at its head office during the year. A random sample of 30 executive level managers reveals the following: Absenteeism: Sample mean = 7.3 days, Sample standard deviation=6.2 days 18 mid-level managers out of the 30 randomly selected mid-level managers, cite stress as a cause of absence. (a) Construct a 90% confidence intervalestimate for the mean number of absences for mid- level managers during the year.(b) Construct a 98% confidence intervalestimate for the population proportion of mid-level managers who cite stress as a cause of absence. (c) What sample size is needed to have 95% confidence in estimating the population mean absenteeism to within 1.5 days if the population standard deviation is estimated to be 8 days? (d) How many mid-level managers need to be selected to have 99% confidence in estimating population proportion of mid-level managers who cite stress as a cause of absence to within +0.075 if no previous estimate is available?

Answer 1

Following are the answer to this question:

Explanation:

Given:

n = 30 is the sample size.

The mean
`\bar X` = 7.3 days.

The standard deviation = 6.2 days.

df = n-1

`= 30-1 \\ =29`

The importance level is
`\alpha` = 0.10

The table value is calculated with a function excel 2010:

`= tinv (\ probility, \ freedom \ level) \\= tinv (0.10,29) \\ =1.699127\\ = t_(al(2x-1))= 1.699127`

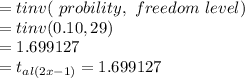
The method for calculating the trust interval of 90 percent for the true population means is:

Formula:

`\bar X - t_(al 2,x-1) (S)/(√(n)) \leq \mu \leq \bar X+ t_(al 2,x-1) (S)/(√(n))`

`=\bar X - t_(0.5, 29) (6.2)/(√(30)) \leq \mu \leq \bar X+ t_(0.5, 29) (6.2)/(√(30))\\\\=7.3 -1.699127 (6.2)/(√(30))\leq \mu \leq7.3 +1.699127 (6.2)/(√(30))\\\\=7.3 -1.699127 (1.13196)\leq \mu \leq7.3 +1.699127 (1.13196) \\\\=5.37 \leq \mu \leq 9.22 \\`

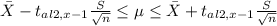
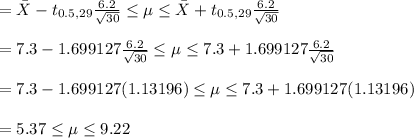
It can rest assured that the true people needs that middle managers are unavailable from 5,37 to 9,23 during the years.