Answer:
The question is incomplete. The complete table is:
Score in percent (X): 80, 75, 70, 90, 95, 100, 75, 60, 75, 95
Time in minute (Y) : 45, 48, 40, 50, 40, 30, 30, 39, 38, 55
The answer is 0.55 %
Explanation:
ΣX = 815
ΣY = 425
ΣX x Y = 34565
Σ = 67925
Σ
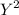 = 18699
= 18699
So, correlation coefficient, b

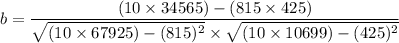
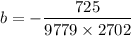
b = -0.0741
Correlation Determination:
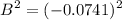
= = 0.0055 = 0.55%
Therefore, 0.55 percentage of the variation in y can be explained by x variable.