Question

Among the four northwestern states, Washington has 51% of the total population, Oregon has 30%, Idaho has 11%, and Montana has 8%. A market researcher selects a sample of 1000 subjects, with 450 in Washington, 340 in Oregon, 150 in Idaho, and 60 in Montana. At the 0.05 significance level, test the claim that the sample of 100 subjects has a distribution that agrees with the distribution of state populations.

Answer 1

Explanation:

From the given information:

the null hypothesis and the alternative hypothesis can be computed as follows:

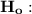`\mathbf{H_o:}` The sample have a distribution that agrees with the distribution of state populations.

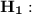`\mathbf{H_1:}` The sample have a distribution that does not agrees with the distribution of state populations.

The Chi-Square test statistics
`\mathbf{X^2 = ((Observed \ value - Expected \ value ))/((Expected \ value ) ^2 )}`

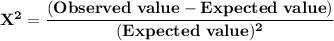
Among the four northwestern states, Washington has 51% of the total population, Oregon has 30%, Idaho has 11%, and Montana has 8%. A market researcher selects a sample of 1000 subjects, with 450 in Washington, 340 in Oregon, 150 in Idaho, and 60 in Montana.

The observed and the expected value can be computed as follows:

States Observed Expected
`X^2 = ((O- E)^2)/(E)`

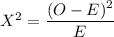
Washington 450 0.51 × 1000 = 510

Oregon 340 0.30 × 1000 = 300

Idaho 150 0.11 × 1000 = 110

Montana 60 0.08 × 1000 = 80

Total 1000 1000

For washington :

`X^2 = ((O- E)^2)/(E)`

`X^2 = ((450 -510)^2)/(510)`

`X^2 = (3600)/(510)`

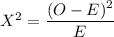
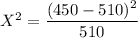
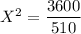
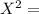`X^(2)=` 7.06

For Oregon

`X^2 = ((O- E)^2)/(E)`

`X^2 = ((340- 300)^2)/(300)`

`X^2 = (1600)/(300)`

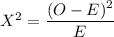
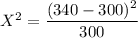
`X^(2)=` 5.33

For Idaho

`X^2 = ((O- E)^2)/(E)`

`X^2 = ((150- 110)^2)/(110)`

`X^2 = (1600)/(110)`

`X^2 =14.55`

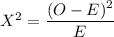
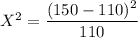
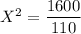
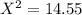
For Montana

`X^2 = ((O- E)^2)/(E)`

`X^2 = ((60- 80)^2)/(80)`

`X^2 = (400)/(80)`

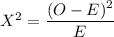
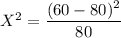
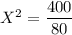
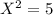`X^2 = 5`.00

The Chi-square test statistics for the observed and the expected value can be computed as follows:

States Observed Expected
`X^2 = ((O- E)^2)/(E)`

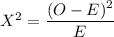
Washington 450 0.51 × 1000 = 510 7.06

Oregon 340 0.30 × 1000 = 300 5.33

Idaho 150 0.11 × 1000 = 110 14.55

Montana 60 0.08 × 1000 = 80 5.00

Total 1000 1000 31.94

The Chi-square Statistics Test
`\mathbf{X^2 = 31.94}`

Degree of freedom = n - 1

Degree of freedom = 4 - 1

Degree of freedom = 3

At 0.05 level of significance, the critical value of :

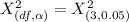`X^2_((df, \alpha) )=X^2_{(3, 0.05)` = 7.815

Decision Rule: To reject null hypothesis if the test statistics is greater than the critical value

Conclusion: We reject the null hypothesis since test statistics is greater than critical value, therefore, we conclude that there is sufficient information to say that the sample has a distribution that does not agrees with the distribution of state populations.