Question

Find the equation of the line in slope-intercept form that passes through the given points (-3,6) and (-1,3).

Answer 1

y=-3/2x

Explanation:

First, find the slope with y2-y1/x2-x1=m

3-6 m=-3/2

--------- =

-1-+-3

Now plug it in to point slope form

Point slope form is y-y1=m(x-x1)

y-3=-3/2(x--1) Distribute -3/2 to x and 1

y-3=-3/2x-3 Add three on both sides to get y alone

y=-3/2x Three's cancel out. This is the final equation.

Answer 2

`\large\boxed{y=-(3)/(2)x+(3)/(2)}`

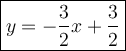
Explanation:

Use the two-points slope equation:
`\boxed{m=(y_(2)-y_(1))/(x_(2)-x_(1))}`

Given the two coordinate points of
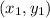`(x_(1), y_(1))` and
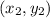`(x_(2), y_(2))`, implement these values into the equation and solve for m.

`m=((3)-(6))/((-1)-(-3))\\\\m=((-3))/((2))\\\\m=-(3)/(2)`

The slope is then placed in the equation - y = -3/2x + b.

Then, insert a value for y and x from the same coordinate point to solve for b.

`6=-(3)/(2)(-3)+b\\\\6=(9)/(2)+b\\\\(3)/(2)=b`

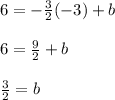
Then, plug it all in to get
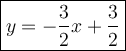`\large\boxed{y=-(3)/(2)x+(3)/(2)}`.