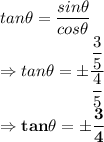Answer:
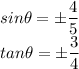
Explanation:
Kindly refer to the attached image of a right angled
 .
.
Let
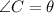
Sides BC = a
AB = c and
AC = b respectively.
To prove:
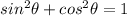
Proof:
Using Sine and Cosine values:
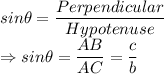
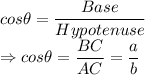
As per Pythagorean theorem:
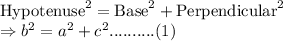
Considering the LHS of
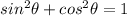 :
:

Now, using equation (1):

Hence, proved that :
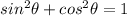
Now, we are given that:
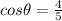
To find, sine and cosine values of the angle i.e.
 and
and
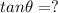
Using
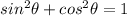 :
:
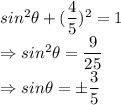
We know that: