Question

An electron from a Ti ^ + 2 hydrogen ion leaps from one orbit with radius 13.25 angstrom to another orbit with radius 2.12 angstrom. determine the energy (Joule) e produced in said transition and the wavelength (in cm)

Answer 1

E = 0.2276 10⁻¹⁹ J , λ = 8.73374 10⁻⁴ cm

Step-by-step explanation:

Bohr's atomic model can be used for hydrogen-type atoms, that is, they have a single electron in their last orbit, this is the case of doubly ionized Titanium.

It is much easier to work in EV units.

r = a₀ / Z n²

E = - 13.606 (Z² / n²)

where ao is the Bohr radius, which is the ground state orbital of hydrogen a₀ = 0.0529 nm, Z is the atomic number of titanium, and n is an integer that represents the different states of the system.

a) Let's look for the energy, for this we look for the integer numbers of these orbits

r = 13.25 A = 1.325 nm

r = a₀ / Z n²

n = √(Z r / a₀)

the atomic number of titanium is Z = 22

n = √ (22 1.325 / 0.0529)

n = 23

r = 2.12 A = 0.212 nm

n = √ (22 0.212 / 0.0529)

n = 9

now we can calculate the energy of the transition

E = 13.606 (1 /
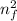`n_(f)^2` - 1 /
`x_(o)^2`)

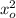E = 13.606 (1/9² - 1/23²)

E = 13.6060 (0.010455)

E = 0.1423 eV

Let's reduce to J

E = 0.1423 eV (1.6 10⁻¹⁹ J / 1eV) = 0.2276 10⁻¹⁹ J

To find the wavelength of the transition, use the Planck relation

E = h f

the relationship of frequency and speed of light

c = λ f

we substitute

E = h c /λ

λ = hc / E

λ = 6.626 10⁻³⁴ 3 10⁸ / 0.2276 10⁻¹⁹

λ = 8.73374 10⁻⁶ m

λ = 8.73374 10⁻⁴ cm