Answer:
(a) The standard deviation of the amount spent is $3229.18.
(b) The probability that a household spends between $4000 and $6000 is 0.2283.
(c) The range of spending for 3% of households with the highest daily transportation cost is $12382.86 or more.
Explanation:
We are given that the average annual amount American households spend on daily transportation is $6312 (Money, August 2001). Assume that the amount spent is normally distributed.
(a) It is stated that 5% of American households spend less than $1000 for daily transportation.
Let X = the amount spent on daily transportation
The z-score probability distribution for the normal distribution is given by;
Z =
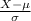 ~ N(0,1)
~ N(0,1)
where,
 = average annual amount American households spend on daily transportation = $6,312
= average annual amount American households spend on daily transportation = $6,312
 = standard deviation
= standard deviation
Now, 5% of American households spend less than $1000 on daily transportation means that;
P(X < $1,000) = 0.05
P(
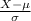 <
<
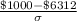 ) = 0.05
) = 0.05
P(Z <
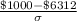 ) = 0.05
) = 0.05
In the z-table, the critical value of z which represents the area of below 5% is given as -1.645, this means;
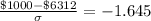
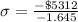 = 3229.18
= 3229.18
So, the standard deviation of the amount spent is $3229.18.
(b) The probability that a household spends between $4000 and $6000 is given by = P($4000 < X < $6000)
P($4000 < X < $6000) = P(X < $6000) - P(X
 $4000)
$4000)
P(X < $6000) = P(
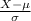 <
<
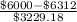 ) = P(Z < -0.09) = 1 - P(Z
) = P(Z < -0.09) = 1 - P(Z
 0.09)
0.09)
= 1 - 0.5359 = 0.4641
P(X
 $4000) = P(
$4000) = P(
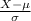
= 1 - 0.7642 = 0.2358
Therefore, P($4000 < X < $6000) = 0.4641 - 0.2358 = 0.2283.
(c) The range of spending for 3% of households with the highest daily transportation cost is given by;
P(X > x) = 0.03 {where x is the required range}
P(
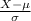 >
>
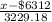 ) = 0.03
) = 0.03
P(Z >
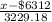 ) = 0.03
) = 0.03
In the z-table, the critical value of z which represents the area of top 3% is given as 1.88, this means;
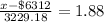
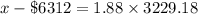
x = $6312 + 6070.86 = $12382.86
So, the range of spending for 3% of households with the highest daily transportation cost is $12382.86 or more.