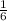Question

A twelve-sided die with sides labeled through will be rolled once. Each number is equally likely to be rolled. What is the probability of rolling a number greater than ? Write your answer as a fraction in simplest form.

Answer 1

Complete Question:

A twelve-sided die with sides labeled 1 through 12 will be rolled once. Each number is equally likely to be rolled, what is the probability of rolling a number greater than 10?

Answer:

`P(T) = (1)/(6)`

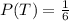
Explanation:

Given

Number of Sides = 12

Required

Probability of obtaining a side greater than 10

We start by listing out the sample space;

`S = \{1,2,3,4,5,6,7,8,9,10,11,12\}`

`n(S) = 12`

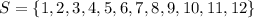
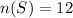
Next, we list out digits greater than 10; Represent this with T

`T = \{11,12\}`

`n(T) = 2`

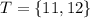
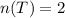
Probability of T is calculated as follows;

`P(T) = (n(T))/(n(S))`

`P(T) = (2)/(12)`

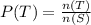
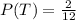
Divide the numerator and denominator by 2

`P(T) = (1)/(6)`

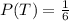
Hence, the required probability is
`(1)/(6)`