Question

Write a polynomial in standard form with the zeros -4,0, 1, and 4.

A. x4 – x3 - 8x2 + 16x
B. x4 – x3 – 16x2 + 16x
C. X4 - 7x3 + 8x2 + 16x
D. x4-9x3 + 24x2 – 16x

Answer 1

Answer:
`x^4-x^3-16x^2+16x`

Explanation:

Factor theorem : If x=a is a zero of a polynomial p(x) then (x-a) is a factor of p(x).

Given: Zeroes of polynomial : -4,0, 1, and 4.

Then Factors =
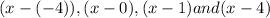`(x-(-4)), (x-0), (x-1) and (x-4)` [By factor theorem ]

`=(x+4), (x-0), (x-1) and (x-4)`

Multiplying these factors to get polynomial in standard form.

`(x+4)*(x-0)*(x-1)*(x-4) \\\\= x(x+4)(x-4)(x-1)\\\\= x(x^2-4^2)(x-1)\\\\= x(x^2-16)(x-1)\\\\= x(x^2-16)(x-1)\\\\=x(x^2x+x^2\left(-1\right)+\left(-16\right)x+\left(-16\right)\left(-1\right))\\\\= x(x^3-x^2-16x+16)\\\\=x^4-x^3-16x^2+16x`

Hence, B is the correct option.