Answer:
The value is

Step-by-step explanation:
From the question we are told that
The wavelength is

The distance of the screen is
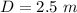
The order of the bright fringes is
 (10 fringe + central maximum = eleven bright fringes )
(10 fringe + central maximum = eleven bright fringes )
The distance between the fringe is

Generally the condition for constructive interference is
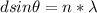
=>

Now from the SOHCAHTOA rule the angle
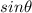 is mathematically represented as
is mathematically represented as

So

=>
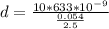
=>
