Answer:
C
Explanation:
So we already know that:
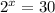
And we want to find the value of:

So, what you want to do here is to separate the exponents. Recall the properties of exponents, where:
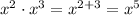
We can do the reverse of this. In other words:
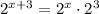
If we multiply it back together, we can check that this statement is true.
Thus, go back to the original equation and multiply both sides by 2^3:
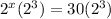
Combine the left and multiply out the right. 2^3 is 8:
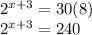
The answer is C.