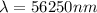Complete Question
You are performing a double slit experiment very similar to the one from DL by shining a laser on two nattow slits spaced
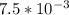 meters apart. However, by placing a piece of crystal in one of the slits, you are able to make it so that the rays of light that travel through the two slits are Ï out of phase with each other (that is to say, Ao,- ). If you observe that on a screen placed 4 meters from the two slits that the distance between the bright spot closest to center of the pattern is 1.5 cm, what is the wavelength of the laser?
meters apart. However, by placing a piece of crystal in one of the slits, you are able to make it so that the rays of light that travel through the two slits are Ï out of phase with each other (that is to say, Ao,- ). If you observe that on a screen placed 4 meters from the two slits that the distance between the bright spot closest to center of the pattern is 1.5 cm, what is the wavelength of the laser?
Answer:
The wavelength is
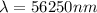
Step-by-step explanation:
From the question we are told that
The distance of slit separation is

The distance of the screen is
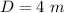
The distance between the bright spot closest to the center of the interference is
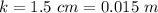
Generally the width of the central maximum fringe produced is mathematically represented as
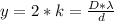
=>

=>
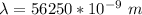
=>