Question

the remains of an ancient ball court include a rectangular playing alley with a perimeter of about 64 M. the length of the alley is 2 times the width. find the length and the width of the playing alley​

Answer 1

The length is 21.3 meters

The width is 10.6 meters

Explanation:

This problem is on the mensuration of flat shapes, a rectangular shape

we are required to solve for the length and width of the rectangular ball court

we know that the perimeter is expressed as

`P= 2(L)+2(W)`

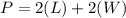
let the width be x

hence the length is 2x

Given data

perimeter = 64 meters

length l= 2x

width w= x

Substituting our data and solving for x we have

`64= 2(2x)+2(x)\\\\64= 4x+2x\\\\64= 6x`

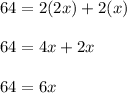
Dividing both sides by 6 we have

`x=(64)/(6)\\\\ x= 10.66`

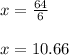
Hence the width is 10.66 meters

The length is 2x= 2(10.66)= 21.33 meters