Question

Area of a triangle two sides of which are 18 cm and 12 cm

and the perimeter is 44 cm.​

Answer 1

`\huge \boxed{\mathrm{83.9 \ cm^2}}`

Explanation:

Two sides of the triangle are given.

The perimeter is given.

We need to solve for the third side.

`P=a+b+c`

`P= \sf perimeter`

`a,b,c= \sf side \ lengths`

`44=18+12+c`

`c=14`

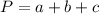
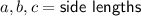
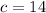
The measure of the third side is 14 cm.

When three sides of the triangle are given, we can solve for the area using Heron’s formula.

`A=√(s(s-a)(s-b)(s-c))`

`s=\sf semi \ perimeter`

`\displaystyle s=(P)/(2) =(44)/(2) =22`

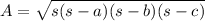
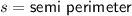
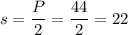
Plugging in the values and evaluating.

`A=√(22(22-18)(22-12)(22-14))`

`A = 83.904708...`

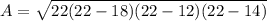
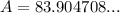
The area of the triangle is approximately 83.9 cm².

Answer 2

≈ 83.9 cm²

Explanation:

Given:

• P = a+b+c = 44 cm
• a = 18 cm
• b = 12 cm

Then:

• c= P -(a+b) = 44 -(18+12) = 14 cm

Area of the triangle is found by using Herons formula:

• A = √s(s-a)(s-b)(s-c),

where s = P/2 = 44/2 = 22 cm

• A = √22(22-18)(22-12)(22-14) = √22*4*10*8= √7040 ≈ 83.9 cm²