A physical pendulum in the form of a planar object moves in simple harmonic motion with a frequency f. The pendulum has a mass m, and the pivot is located a distance d from the c…

Question

asked Jun 2, 2021 53.4k views

1 Answer

Marco Leung · Answer 1 · 2021-06-06T15:16:47+0000

Answer:

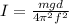
$I = (mgd)/(4\pi^(2)f^(2))$

Step-by-step explanation:

The moment of inertia (I) of the pendulum can be found using the following equation:

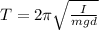
$T = 2\pi\sqrt{(I)/(mgd)}$

Where:

T: is the period of the pendulum

m: is the pendulum's mass

g: is the gravity

d: is the distance of the pivot from the center of mass

Solving the above equation for I:

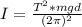$I = (T^(2)*mgd)/((2\pi)^(2))$ (1)

We have that the pendulum moves in simple harmonic motion with a frequency f, and this f is equal to:

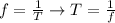
$f = (1)/(T) \rightarrow T = (1)/(f)$

By entering T into equation (1) we have:

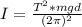
$I = (T^(2)*mgd)/((2\pi)^(2))$

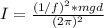
$I = ((1/f)^(2)*mgd)/((2\pi)^(2))$

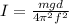
$I = (mgd)/(4\pi^(2)f^(2))$

Therefore, the moment of inertia of the pendulum about the pivot point is
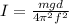$I = (mgd)/(4\pi^(2)f^(2))$ .

I hope it helps you!