Question

A 121-kg astronaut (including space suit) acquires a speed of 2.90 m/s by pushing off with her legs from a 1600-kg space capsule. Use the reference frame in which the capsule is at rest before the push.

A) What is the velocity of the space capsule after the push in the reference frame?
B) If the push lasts 0.660 s , what is the magnitude of the average force exerted by each on the other?
C) What is the kinetic energy of the astronaut after the push in the reference frame?
D) What is the kinetic energy of the capsule after the push in the reference frame?

Answer 1

a) 0.22 m/s

b) 531.67 N

c) 508.81 J

d) 38.72 J

Step-by-step explanation:

the mass of the astronaut = 121 kg

astronaut's push of speed = 2.9 m/s

mass of the space capsule = 1600 kg

a) according to the conservation of momentum, the summation of the total momentum in a system must be equal to zero.

let us take the direction of the astronaut as positive.

Astronaut's momentum p = mv

where

m is the mass

v is the velocity

momentum p = 121 x 2.9 = 350.9 kg-m/s

The space capsules momentum = mv

==> 1600 x (-v) = -1600v this is because the space capsule moves in the opposite direction to the astronaut.

according to conservation of momentum

350.9 + (-1600v) = 0

350.9 = 1600v

v = 350.9/1600 = 0.22 m/s

b) magnitude of the force F is the rate of change of momentum.

The astronaut and the space capsule both change momentum from 0 to 350.9 kg-m/s. In 0.66 seconds, the force will be

F =
`(m(v - u))/(t)`

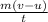
where

u is their initial velocity = 0 m/s

where v = 2.9

t = 0.66

substituting, we have

F =
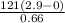`(121(2.9 - 0))/(0.66)` = 350.9/0.66 = 531.67 N this same force is experienced by the space capsule

c) Kinetic energy of the astronaut =
`(1)/(2) mv^(2)`

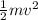
m is the mass = 121 kg

v is the velocity = 2.9 m/s

KE =
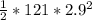`(1)/(2)*121*2.9^(2)` = 508.81 J

d) Kinetic energy of the space capsule =
`(1)/(2) mv^(2)`

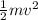
KE =
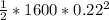`(1)/(2)* 1600* 0.22^(2)` = 38.72 J