Question

You've recently read about a chemical laser that generates a 20.0-cm-diameter, 26.0 MW laser beam. One day, after physics class, you start to wonder if you could use the radiation pressure from this laser beam to launch small payloads into orbit. To see if this might be feasible, you do a quick calculation of the acceleration of a 20.0-cm-diameter, 110 kg, perfectly absorbing block.

Required:
a. What speed would such a block have if pushed horizontally 100 m along a frictionless track by such a laser?
b. Does this seem like a promising method for launching satellites?

Answer 1

(a). The speed of the block is 0.395 m/s.

(b). No

Explanation :

Given that,

Diameter = 20.0 cm

Power = 26.0 MW

Mass = 110 kg

diameter = 20.0 cm

Distance = 100 m

We need to calculate the pressure due to laser

Using formula of pressure

`P_(r)=(I)/(c)`

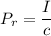
`P_(r)=(P)/(Ac)</p><p>Put the value into the formula</p><p>[tex]P_(r)=(26.0*10^(6))/(\pi*(10*10^(-2))^2*3*10^(8))`

`P_(r)=2.75\ N/m^2`

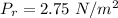
We need to calculate the force

Using formula of force

`F=P* A`

`F=P* \pi r^2`

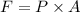
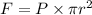
Put the value into the formula

`F=2.75*\pi (0.01)^2`

`F=0.086\ N`

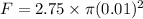
We need to calculate the acceleration

Using formula of force

`F=ma`

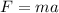
Put the value into the formula

`0.086=110* a`

`a=(0.086)/(110)`

`a=0.000781\ m/s^2`

`a=7.81*10^(-4)\ m/s^2`

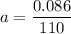
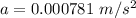
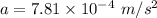
(a). We need to calculate speed of the block

Using equation of motion

`v^2=u^2+2ad`

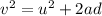
Put the value into the formula

`v=\sqrt{2*7.81*10^(-4)*100}`

`v=0.395\ m/s`

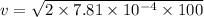
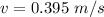
(b). No because the velocity is very less.

Hence, (a). The speed of the block is 0.395 m/s.

(b). No