Question

A 0.40 kg mass hangs on a spring with a spring constant of 12 N/m. The system oscillated with a constant amplitude of 12 cm. What is the maximum acceleration of the system

Answer 1

The maximum acceleration of the system is 359.970 centimeters per square second.

Step-by-step explanation:

The motion of the mass-spring system is represented by the following formula:

`x(t) = A\cdot \cos (\omega \cdot t + \phi)`

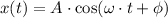
Where:

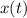`x(t)` - Position of the mass with respect to the equilibrium position, measured in centimeters.

`A` - Amplitude of the mass-spring system, measured in centimeters.

`\omega` - Angular frequency, measured in radians per second.

`t` - Time, measured in seconds.

`\phi` - Phase, measured in radians.

The acceleration experimented by the mass is obtained by deriving the position equation twice:

`a (t) = -\omega^(2)\cdot A \cdot \cos (\omega\cdot t + \phi)`

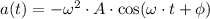
Where the maximum acceleration of the system is represented by
`\omega^(2)\cdot A`.

The natural frequency of the mass-spring system is:

`\omega = \sqrt{(k)/(m) }`

Where:

`k` - Spring constant, measured in newtons per meter.

`m` - Mass, measured in kilograms.

If
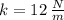`k = 12\,(N)/(m)` and
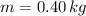`m = 0.40\,kg`, the natural frequency is:

`\omega = \sqrt{(12\,(N)/(m) )/(0.40\,kg) }`

`\omega \approx 5.477\,(rad)/(s)`

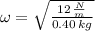
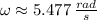
Lastly, the maximum acceleration of the system is:

`a_(max) = \left(5.477\,(rad)/(s))^(2)\cdot (12\,cm)`

`a_(max) = 359.970\,(cm)/(s^(2))`

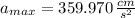
The maximum acceleration of the system is 359.970 centimeters per square second.