Answer:
Explained below.
Explanation:
(10)
The data set is:
S = {124, 94, 129, 109, 114}
The mean and standard deviation are:
![\bar x=(1)/(n)\sum x=(1)/(5)* [124+94+...+114]=114\\\\s=\sqrt{(1)/(n-1)\sum ( x-\bar x)^(2)}](https://img.qammunity.org/2021/formulas/mathematics/college/ec5yg03g79f0znttj1nlcs2sxm5qykh1u5.png)
![=\sqrt{(1)/(5-1)* [(124-114)^(2)+(94-114)^(2)+...+(114-114)^(2)]}\\=\sqrt{(750)/(4)}\\=13.6931\\\approx 13.69](https://img.qammunity.org/2021/formulas/mathematics/college/prs83wn902zvkcofhylk9398ghgdutpotl.png)
The correct option is B.
(11)
According to the Empirical 95% of the data for a Normal distribution are within 2 standard deviations of the mean.
So, the adult male's height is in the same range as about 95% of the other adult males whose heights were measured.
The correct option is B.
(12)
Let the score be X.
Given:
μ = 100
σ = 26
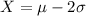
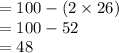
The correct option is B.
(13)
Let X be the prices of a certain model of new homes.
Given:
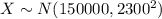
Compute the percentage of buyers who paid between $147,700 and $152,300 as follows:
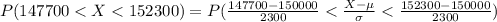
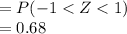
According to the 68-95-99.7, 68% of the data for a Normal distribution are within 1 standard deviations of the mean.
The correct option is D.
(14)
Compute the percentage of buyers who paid more than $154,800 as follows:
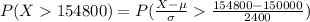
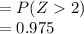
According to the 68-95-99.7, 95% of the data for a Normal distribution are within 2 standard deviations of the mean. Then the percentage of data above 2 standard deviations of the mean will be 97.5% and below 2 standard deviations of the mean will be 2.5%.
The correct option is D.
(15)
The z-score is given as follows:
