Answer:
The mean and standard deviation of the number of correct answers is 3 and 1.55 respectively.
Explanation:
We are given that a quiz consists of 15 multiple choice questions, each with five possible answers, only one of which is correct.
Let X = the number of correct answers
The above situation can be represented through binomial distribution;
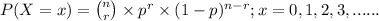
where, n = number of samples (trials) taken = 15 multiple choice questions
r = number of success
p = probability of success which in our question is probability of
one correct answer out of 5, i.e; p =
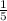 = 0.2
= 0.2
So, X ~ Binom(n = 15, p = 0.2)
Now, the mean of the number of correct answers is given by;
Mean of X, E(X) =
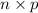
=
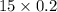 = 3
= 3
And the standard deviation of the number of correct answers is given by;
Standard deviation, S.D.(X) =
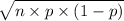
=
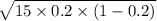 = 1.55
= 1.55