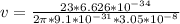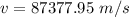Question

A. What quantum number of the hydrogen atom comes closest to giving a 61-nm-diameter electron orbit?

b. What are the electron's speed and energy in this state?

Answer 1

a

`n = 23`

b

`v = 87377.95 \ m/s`

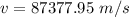
Step-by-step explanation:

From the question we are told that

The diameter is
`d = 61\ nm = 61 *10^(-9) \ m`

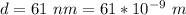
Generally the radius electron orbit is mathematically represented as

`r = (61 *10^(-9))/(2)`

=>
`r = 3.05*10^(-8) \ m`

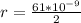
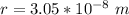
This radius can also be represented mathematically as

`r = n^2 * a_o`

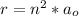
Here n is the quantum number and
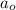`a_o` is the Bohr radius with a value

`a_o = 0.0529 *10^(-9) \ m`

So

`n = \sqrt{(3.05*10^(-8))/( 0.059*10^(-9)) }`

=>
`n = 23`

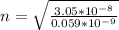
Generally the angular momentum of the electron is mathematically represented as

`L = m * v * r = (n * h )/(2 \pi)`

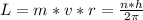
Here h is the Planck constant and the value is
`h = 6.626*10^(-34) J \cdot s`

m is the mass of the electron with values
`m = 9.1*10^(-31) \ kg`

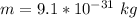
So

`v = (23 * 6.626*10^(-34) )/(2\pi * 9.1 *10^(-31) * 3.05*10^(-8) )`

`v = 87377.95 \ m/s`