Answer:
B A and C
Step-by-step explanation:
Given:
Specimen σ
 σ
σ
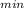
A +450 -150
B +300 -300
C +500 -200
Solution:
Compute the mean stress
σ
 = (σ
= (σ
 + σ
+ σ
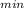 )/2
)/2
σ
 = (450 + (-150)) / 2
= (450 + (-150)) / 2
= (450 - 150) / 2
= 300/2
σ
 = 150 MPa
= 150 MPa
σ
 = (300 + (-300))/2
= (300 + (-300))/2
= (300 - 300) / 2
= 0/2
σ
 = 0 MPa
= 0 MPa
σ
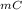 = (500 + (-200))/2
= (500 + (-200))/2
= (500 - 200) / 2
= 300/2
σ
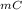 = 150 MPa
= 150 MPa
Compute stress amplitude:
σ
 = (σ
= (σ
 - σ
- σ
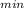 )/2
)/2
σ
 = (450 - (-150)) / 2
= (450 - (-150)) / 2
= (450 + 150) / 2
= 600/2
σ
 = 300 MPa
= 300 MPa
σ
 = (300- (-300)) / 2
= (300- (-300)) / 2
= (300 + 300) / 2
= 600/2
σ
 = 300 MPa
= 300 MPa
σ
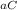 = (500 - (-200))/2
= (500 - (-200))/2
= (500 + 200) / 2
= 700 / 2
σ
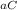 = 350 MPa
= 350 MPa
From the above results it is concluded that the longest fatigue lifetime is of specimen B because it has the minimum mean stress.
Next, the specimen A has the fatigue lifetime which is shorter than B but longer than specimen C.
In the last comes specimen C which has the shortest fatigue lifetime because it has the higher mean stress and highest stress amplitude.