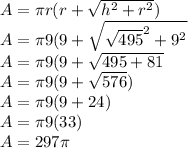Answer:
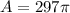
Explanation:
To solve this problem we need to be familiar with the formula for the surface area of a cone:
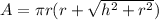
We are given the length of a side and the diameter, to calculate the radius divide the diameter in half:
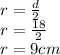
To calculate the height of the cone, we must use the Pythagorean Theorem:
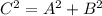
We can treat the side length as the hypotenuse
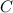 , the radius as the base
, the radius as the base
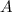 , and solve for height
, and solve for height
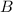 . Set the expression up like this:
. Set the expression up like this:
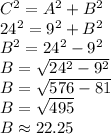
Now we can plug into our original formula: