Answer:
Equation :
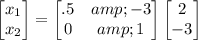
Explanation:
To isolate the following matrix, we will have to divide either by matrix 1, or the co - efficient of the matrix shown below. By doing so we will have to take the inverse of the co - efficient of that same matrix on the other side. In other words,
 - Matrix which we have to isolate,
- Matrix which we have to isolate,
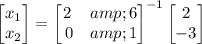 - Equation used to solve the matrix
- Equation used to solve the matrix
Now as you can see this equation is not any of the given options. That is as we have to simplify it a bit further,

We know that 1 / 2 can be replaced with 0.5, giving us the following equation to solve for x1 and x2,
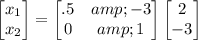
As you can see our solution is option d.