Question

The atomic mass number of copper is A=64. Assume that atoms in solid copper form a cubic crystal lattice. To envision this, imagine that you place atoms at the centers of tiny sugar cubes, then stack the little sugar cubes to form a big cube. If you dissolve the sugar, the atoms left behind are in a cubic crystal lattice. What is the smallest distance between two copper atoms?

Answer 1

0.228 nm

Step-by-step explanation:

Atomic mass number of copper = 64

but an atomic mass unit = 1.66 x 10^-27 kg

therefore, the mass of the copper atom m = 64 x 1.66 x 10^-27 kg = 1.06 x 10^-25 kg

The number of atoms in this mass n = ρ/m

where ρ is the density of copper = 8.96 x 10^3 kg/m^3

==> n = (8.96 x 10^3)/(1.06 x 10^-25) = 8.45 x 10^28 atoms/m^3

We know that the volume occupied by this amount of atoms n =
`a^(3)`

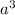
where a is the lattice constant

equating, we have

8.45 x 10^28 =
`a^(3)`

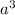
a = 4.389 x 10^9

we also know that

d = 1/a

where d is the smallest distance between the two copper atom.

d = 1/(4.389 x 10^9) = 2.28 x 10^-10 m

==> 0.228 nm