Question

Find the area of the region between the curve y= 2ln(x) and the horizontal axis for 1<= x <= 4

Answer 1

5.09 units

Explanation:

Given equation

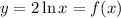`y=2\ln x=f(x)` in the interval
`1\le x\le 4`

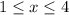
So we integrate
`y` in the given interaval

`\int f(x)=2\int\limits^4_1 {\ln x}dx`

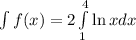
Let us integrate
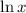`\ln x` first.

let

`u=\ln x, dv=dx`

`du=(1)/(x), v=x`

`\int\ln x dx=udv`

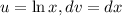
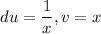
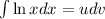
Using integration by parts we get

`uv-\int vdu`

`=x\ln x-\int x(1)/(x)dx`

`=x\ln x-dx`

`=x\ln x-x+C`

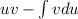
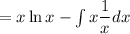
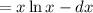
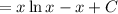
So here

`\int f(x)=2\int\limits^4_1 {\ln x}dx\\ =2(x\ln x-x)_1^4\\ =2[(4\ln 4-4)-(1\ln 1-1)]\\ =2[4\ln 4-4+1]\\ =5.09\ units`

The area of the the region between the curve and horizontal axis is 5.09 units.