Answer:
Decision rule : The p-value <
 so the null hypothesis is rejected
so the null hypothesis is rejected
The test statistics is

The manger will not be manager be satisfied that the company is not under-filling since the company is under-filling its cups
Explanation:
From the question we are told that
The sample size is n = 16
The sample mean is
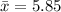
The standard deviation is
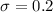
The null hypothesis is
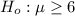
The alternative hypothesis is
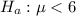
The level of significance is

Generally the test statistics is mathematically represented as

=>
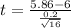
=>

The p-value is obtained from the z-table the value is
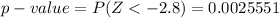
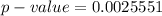
Given that the
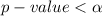 we reject the null hypothesis
we reject the null hypothesis
Hence there is sufficient evidence to support the concern of the quality control manager. and the manger will not be satisfied that since the test proof that the company is under-filling its cups