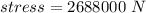Question

On a day that the temperature is 10.0°C, a concrete walk is poured in such a way that the ends of the walk are unable to move. Take Young's modulus for concrete to be 7.00 109 N/m2 and the compressive strength to be 2.00 109 N/m2. (The coefficient of linear expansion of concrete is 1.2 10-5(°C−1).)

What is the stress in the cement on a hot day of 42.0°C? N/m2

Answer 1

The stress is
`stress = 2688000 \ N`

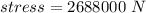
Step-by-step explanation:

From the question we are told that

The first temperature is
`T_1 = 10 ^o \ C`

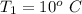
The young modulus is
`Y = 7.00 *10^9\ N/m^2`

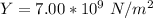
The compressive strength is
`\sigma = 2.00 *10^(9) \ N/m^2`

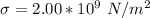
The coefficient of linear expansion is
`\alpha = 1.2 *10^(-5) \ ^o C ^(-1)`

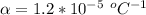
The second temperature is
`T_2 = 42.0^o \ C`

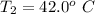
Generally the change in length of the concrete is mathematically represented as

`\Delta L = \alpha * L * [T_2 - T_1 ]`

=>
`(\Delta L)/(L) = \alpha * [T_2 - T_1 ]`

=>
`strain = \alpha * [T_2 - T_1 ]`

Now the young modulus is mathematically represented as

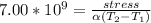
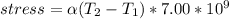
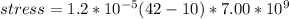
`Y = (stress)/(strain)`

=>
`7.00 *10^9 = (stress)/(\alpha(T_2 - T_1 ) )`

=>
`stress = \alpha (T_2 - T_1 ) * 7.00 *10^9`

=>
`stress = 1.2* 10^(-5) (42 - 10 ) * 7.00 *10^9`

=>
`stress = 2688000 \ N`