Question

If $(ax+b)(2x+3)=20x^2+44x+21$, where $a$ and $b$ are two distinct integers, what is the value of the sum $a+b$?

Answer 1

Answer: 17

Explanation:

Given:
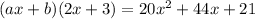`(ax+b)(2x+3)=20x^2+44x+21`, where a and b are two distinct integers.

First simplify left hand side as

`(ax+b)(2x+3)=ax\cdot \:2x+ax\cdot \:3+b\cdot \:2x+b\cdot \:3\\\\=2axx+3ax+2bx+3b\\\\=2ax^2+(3a+2b)x+3b`

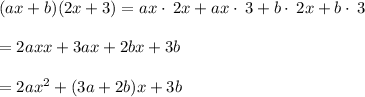
Then comparing left side and right side

`2ax^2+(3a+2b)x+3b=20x^2+44x+21`

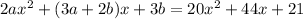
we get 2a = 20 (coefficient of
`x^2`) , and 3b = 21 (constant term)

⇒ a= 10 and b= 7

Then, a+b= 10+7=17

Hence, the value of sum a+b is 17.