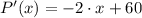Question

The cost and revenue are defined, in dollars, as C(x) = 30x + 100 and R(x) = -x2 + 90x.

Required:
a. Find and simplify the profit function, defined by P(x).
b. Use a. to find the marginal profit function.

Answer 1

a) The profit function is
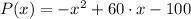`P(x) = -x^(2)+60\cdot x -100`, b) The marginal profit function is
`P'(x) = -2\cdot x + 60`.

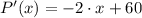Explanation:

a) Let be
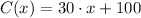`C(x) = 30\cdot x + 100` (cost function) and
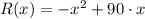`R(x) = -x^(2)+90\cdot x` (revenue function), the profit function is found by subtracting the cost function from the revenue function. That is:

`P(x) = R(x)-C(x)`

`P(x) = -x^(2)+90\cdot x -(30\cdot x + 100)`

`P(x) = -x^(2)+90\cdot x -30\cdot x -100`

`P(x) = -x^(2)+60\cdot x -100`

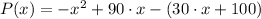
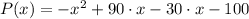
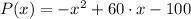
b) The marginal profit function is the first derivative of the profit function:

`P'(x) = -2\cdot x + 60`