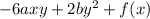Question

The u velocity component of a steady, two-dimensional, incompressible flow field is u = 3 ax 2 - 2 bxy, where a and b are constants. Velocity component v is unknown. Generate an expression for u as a function of x and y.

Answer 1

The velocity component v is
`-6axy+2by^2+f(x)`

Step-by-step explanation:

Given that,

The velocity component of a steady, two-dimensional

`u=3ax^2-2bxy`

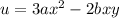
We need to calculate the function of x

Using given equation

`u=3ax^2-2bxy`

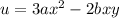
Where, a and b is constant

On differential

`(du)/(dx)=6ax-2by`

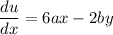
We need to calculate the velocity component v

Using equation of velocity

`(dv)/(dy)=-(du)/(dx)-(dw)/(dz)`

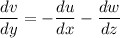
Put the value into the formula

`(dv)/(dy)=-6ax+2by-0`

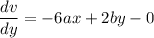
Now, on integration w.r.t y

`v=-6axy+2by^2+f(x)`

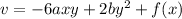
Hence, The velocity component v is
`-6axy+2by^2+f(x)`