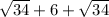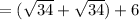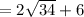Question

The perimeter of the polygon shown in the figure is _______. Question 9 options: 204 units 2√34 +6 units 15 units 30 units

Answer 1

2√34 +6 units

Step-by-step explanation: I took the test

Answer 2

`2√(34) + 6 units`

Explanation:

The perimeter of the polygon shown = AC + BC + AB

Using distance formula, calculate the distance formula,
`d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`, calculate AC, BC, and AB.

The coordinates of the points are as follows,

A(3, 5),

B(0, 0)

C(6, 0)

Find AB:

`d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

Where,

A(3, 5) => (x1, y1)

B(0, 0) => (x2, y2)

`AB = √((0 - 3)^2 + (0 - 5)^2)`

`AB = √((-3)^2 + (-5)^2) = √(9 + 25) = √(34)`

`AB = √(34) units`

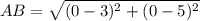
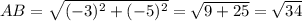
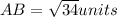
Find BC:

BC is easy to determine from the graph directly. The distance from point B to C, is 6 units.

Find AC:

`d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

Where,

A(3, 5) => (x1, y1)

C(6, 0) => (x2, y2)

`AC = √((6 - 3)^2 + (0 - 5)^2)`

`AB = √((3)^2 + (-5)^2) = √(9 + 25) = √(34)`

`AC = √(34) units`

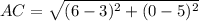
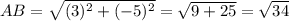
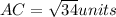
Perimeter of the polygon =
`√(34) + 6 + √(34)`

`= (√(34) + √(34)) + 6`

`= 2√(34) + 6`