Question

What is the freezing point of an aqueous glucose solution that has 25.0 g of glucose?

Answer 1

`T_f=-2.58\°C`

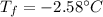
Step-by-step explanation:

Hello,

In this case, we can compute the the freezing point depression by using the following formula:

`T_f-T_0=-i*m*Kf`

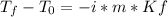
Whereas the freezing point of pure water is 0 °C van't Hoff factor for glucose is 1, the molality is computed as shown below and the freezing point constant of water is 1.86 °C/m:

`m=(25.0g\ glucose*(1mol\ glucose)/(180g\ glucose) )/(100g*(1kg)/(1000g) )\\ \\m=1.39m`

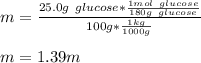
Thus, the freezing point of the solution is:

`T_f=T_0-i*m*Kf\\\\T_f=0\°C-1*1.39m*1.86(\°C)/(m)\\ \\T_f=-2.58\°C`

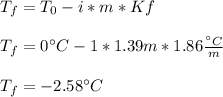
Regards.