Question

1. At the end of the day, a bakery gives everything that is unsold to food banks for the needy. If it has 12 apple pies left at the end of a given day, in how many different ways can it distribute these pies among six food banks for the needy?

2. In how many different ways can the bakery distribute the 12 apple pies if each of the six food banks is to receive at least one pie?

Answer 1

The answer ix below

Step-by-step explanation:

There are 12 apple pies left.

Given that:

n = number of apple pies left = 12

x = number of food banks = 6

1) For the 12 apple pies to be distributed among 6 food banks. The number of ways in which this can be done is:

C(n + x - 1, x - 1) = C(12 + 6 -1, 6 - 1) = C(17, 5) =
`(17!)/((17-5)!5!) =(17!)/(12!5!)=6188 \ ways`

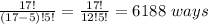
12 apple pies can be distributed among 6 food banks in 6188 ways

2) For the 12 apple pies to be distributed among 6 food banks if each food bank must receive one pie, 6 pies would be remaining. The number of ways in which this can be done is:

C((n - x) + x - 1, n - x) = C(12 - 6 + 6 - 1, 12 - 6) = C(11, 6) =
`(11!)/((11-6)!6!) =(11!)/(6!5!)=462 \ ways`

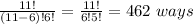
12 apple pies can be distributed among 6 food banks if each food bank must receive one pie in 462 ways