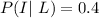Question

Directions: Type your solutions into this document and be sure to show all steps for arriving at your solution. Just giving a final number may not receive full credit.

PROBLEM 1
A website reports that 70% of its users are from outside a certain country, and 60% of its users log on the website every day. Suppose that for its users from inside the country, that 80% of them log on every day. What is the probability that a person is from the country given that he logs on the website every day? Has the probability that he is from the country increased or decreased with the additional information?

Answer 1

The probability is
`P(I | \ L ) =0.4`

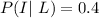
Yes with the additional information that the person logs on everyday the probability increased from
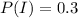`P(I) = 0.3` to
`P(I | L ) = 0.4`

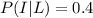
Explanation:

From the question we are told that

The probability that the user is from outside the country is
`P(O) = 0.7`

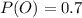
The probability that the user log on everyday is
`P(L) = 0.6`

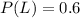
The probability that the user log on everyday and he/she is from inside the country is
`P(L| I) = 0.80`

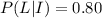
Generally using Bayes theorem the the probability that a person is from the country given that he logs on the website every day is mathematically represented as

`P(I | \ L ) = ( P(L|I) * P(I))/( P(L))`

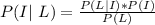
Here
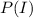`P(I)` is the probability that the person log on every day and it is mathematically evaluated as

`P(I) = 1 - P(O)`

`P(I) = 1 - 0.7`

`P(I) = 0.3`

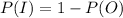
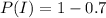
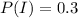
So

`P(I | \ L ) = ( 0,8 * 0.3)/( 0.6)`

`P(I | \ L ) =0.4`