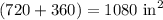Question

A cube and a square pyramid were joined to form the composite solid. A cube with side lengths of 12 inches. A square pyramid with triangular sides with a height of 9 inches. What is the total surface area of the composite solid? 792 square inches 936 square inches 1,080 square inches 1,152 square inches P.S. Yes, I know 100 points, i'm pretty generous, lol

Answer 1

total surface area = 936 in²

Explanation:

total surface area = surface area of the pyramid + surface area of the cube

1. surface area of the pyramid = 4 * area of lateral triangle side

area of lateral triangle side = 12 * 9 /

area of lateral triangle side = 54 in²

2. surface area of the pyramid = 4 * 54

surface area of the pyramid = 216 in²

3. surface area of the cube = 5 * (12 x 12)

-surface area of the cube = 720 in²

therefore, the total surface area = 216 in² + 720 in²

total surface area = 936 in²

Answer 2

C

Explanation:

Please refer to the given picture (sorry, it's a rather bad drawing.)

Anyways, we know that the cube has side lengths of 12. Since the figure is a cube, all the side lengths are 12. Let's find the surface area of the cube first.

The cube has six faces. However, we only need to do five faces because one of the faces is the face that connects the cube to the pyramid. Because of this, we won't count it towards the surface area. Therefore, the total surface area of the cube would be:

`5(bh)`

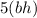
The bh represents the area of one face. The five multiplies that amount by five, giving us the surface area of the cube. Plug in 12 for the base and 12 for the height:

`5(12)(12)=5(144)=720`

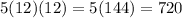
Therefore, the surface area of the cube (excluding one face) is 720 square inches.

Now, find the surface area of the square pyramid. The square pyramid is composed of four congruent triangles and one square base. Again, since the square base is connecting it to the cube, we won't count it. So, we only need to find the area of the four triangles and then add it to 720.

We are given that the height of the pyramid is 9. The base of all four triangles is 12 (since the side length of the cube is 12). However, to find the area, we first need to use the Pythagorean Theorem to determine x or the actual height of one of the triangles. We won't use 9 as the height because the 9 doesn't represent the height of the triangle, but rather of the pyramid. x is essentially the hypotenuse here. Thus:

Pythagorean Theorem:

`a^2+b^2=c^2`

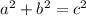
Plug in 9 for a, 12 for b, and x for c:

`9^2+12^2=x^2\\x^2=81+144=225\\x=√(225)=15`

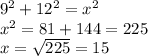
Therefore, the height of the triangles is 15. Now, we can use the area formula for triangles:

`A=(1)/(2) bh`

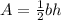
The base is 12 and the height is 15. Thus:

`A=(1)/(2)(12)(15)=6(15)=90`

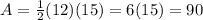
And there are four of them, so the total surface area is:

`4(90)=360`

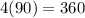
Therefore, the total surface area of the composite figure (excluding the one face) is:

`(720+360)=1080\text{ in}^2`