Question

I need help ASAP
Integrated math II

Answer 1

`\boxed{ \bold{ \sf{x = 16}}}`

`\boxed{ \bold{ \sf{m < AFD = 82}}}`

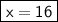
Explanation:

`\sf{5x + 18 = 3x + 50}`

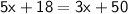
( Being vertically opposite angles)

Vertically opposite angles are always equal.

Move variable to L.H.S and change it's sign

Similarly, Move constant to R.H.S and change it's sign

⇒
`\sf{5x - 3x = 50 - 18}`

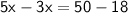
Collect like terms

⇒
`\sf{2x = 50 - 18}`

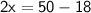
Subtract 18 from 50

⇒
`\sf{2x = 32}`

Divide both sides of the equation by 2

⇒
`\sf{ (2x)/(2) = (32)/(2) }`

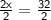
Calculate

⇒
`\sf{x = 16}`

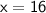
The value of x is 16

Now, let's find value of m<AFD :

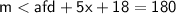`\sf{m < afd + 5x + 18 = 180}` ( sum of angle in straight line )

plug the value of x

⇒
`\sf{m < AFD + 5 * 16 + 18 = 180}`

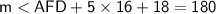
Multiply the numbers

⇒
`\sf{m < AFD + 80 + 18 = 180}`

Add the numbers

⇒
`\sf{m < AFD + 98 = 180}`

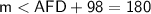
Move constant to R.H.S and change it's sign

⇒
`\sf{m < AFD = 180 - 98}`

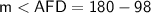
Subtract 98 from 180

⇒
`\sf{m < AFD = 82}`

Value of m<AFD = 82

Hope I helped!

Best regards!!