Question

Find the eccentricity, b. identify the conic, c. give an equation of the directrix, and d. sketch the conic.

r=12/3--10 Cosθ

Answer 1

a) 10/3

b) hyperbola

c) x = ± 6/5

Explanation:

a) A conic section with a focus at the origin, a directrix of x = ±p where p is a positive real number and positive eccentricity (e) has a polar equation:

`r=(ep)/(1\pm e*cos\theta)`

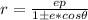
Given the conic equation:
`r=(12)/(3-10cos\theta)`

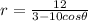
We have to make it to be in the form
`r=(ep)/(1\pm e*cos\theta)`:

`r=(12)/(3-10cos\theta)\\\\multiply\ both\ sides\ by\ (1)/(3) \\\\r=(12*(1)/(3))/((3-10cos\theta)*(1)/(3))\\\\r=(12*(1)/(3))/(3*(1)/(3)-10cos\theta*(1)/(3))\\\\r=(4)/(1-(10)/(3)cos\theta ) \\\\r=((10)/(3)((6)/(5) ) )/(1-(10)/(3)cos\theta )`

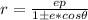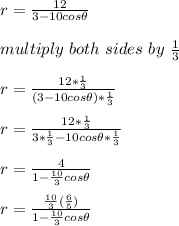
Comparing with
`r=(ep)/(1\pm e*cos\theta)`

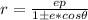
e = 10/3 = 3.3333, p = 6/5

b) since the eccentricity = 3.33 > 1, it is a hyperbola

c) The equation of the directrix is x = ±p = ± 6/5