Question

Determine the equation of the circle graphed below.

screenshot is below - from delta math

Answer 1

`\displaystyle \large{(x-5)^2+(y-2)^2=25}`

Explanation:

Given:

• Center = (5,2)
• Endpoint = (8,6)

First, find radius via distance between center and endpoint. The formula of distance between two points is:

`\displaystyle \large{√((x_2-x_1)^2+(y_2-y_1)^2)}`

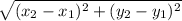
Determine:

• 
  `\displaystyle \large{(x_1,y_1)=(5,2)}`
• 
  `\displaystyle \large{(x_2,y_2)=(8,6)}`

Hence:

`\displaystyle \large{√((8-5)^2+(6-2)^2)}\\\displaystyle \large{√((3)^2+(4)^2)}\\\displaystyle \large{√(9+16) = √(25) = 5}`

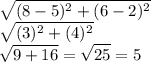
Therefore, the radius is 5.

Then we can substitute center and radius in circle equation. The equation of a circle is:

`\displaystyle \large{(x-h)^2+(y-k)^2=r^2}`

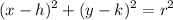
Our center is at (h,k) which is (5,2) and radius beings 5.

Hence, your answer is:

`\displaystyle \large{(x-5)^2+(y-2)^2=25}`