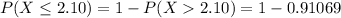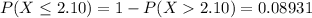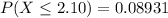Complete Question
One consequence of the popularity of the internet is that it is throughout to reduce television watching. Suppose that a random sample of 55 individuals who consider themselves to be avid Internet users results in a mean time of 2.10 hours watching television on a weekday. The standard deviation is
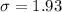
Required:
Determine the likelihood of obtaining a sample mean of 2.10 hours or less from a population whose mean is presumed to be 2.45 hours.
Answer:
The likelihood is
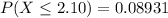
Explanation:
From the question we are told that
The sample size is

The population mean is
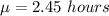
The random mean considered

Generally the standard error of mean is mathematically represented as
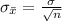
=>
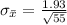
=>
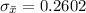
The likelihood of obtaining a sample mean of 2.10 hours or less from a population whose mean is presumed to be 2.45 hours is mathematically represented as
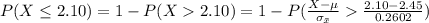
Generally


From the z-table the value of
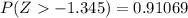
So