A customer deposits $500 in an account that pays 5% annual interest.
What is the balance after 3 years if the interest is compounded annually? Round your answer to the nearest cent.
Compound interest formula:
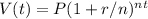
t = years since initial deposit
n = number of times compounded per year
r = annual interest rate (as a decimal)
P = initial (principal) investment
V(t) = value of investment after t years