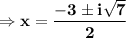Answer:
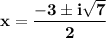
Explanation:
Given quadratic equation is:
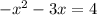
Rewriting the given equation:
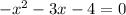
OR
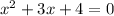
Solution of a quadratic equation represented as
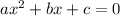 is given as:
is given as:
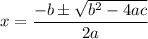
Comparing the given equation with standard equation:
a = 1
b = 3
c = 4
So, the roots are:
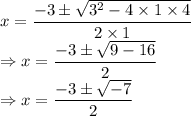
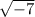 can be written as
can be written as
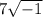
and
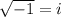
So,
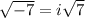
The numbers containing
 in them, are called as complex numbers.
in them, are called as complex numbers.
Therefore, the roots of the equation can be written as: