Question

How much time does a bike with an acceleration of 2ms-2 take to increase its velocity from 10ms-1 to 30ms-1?​

Answer 1

`\boxed{\sf Time \ taken = 10 \ seconds}`

Given:

Initial velocity (u) = 10 m/s

Final velocity (v) = 30 m/s

Acceleration (a) = 2 m/s²

To Find:

Time taken (t) by bike to increase its velocity from 10 m/s to 30 m/s with an acceleration of 2 m/s²

Step-by-step explanation:

`\sf From \ equation \ of \ motion:`

`\boxed{ \bold{v = u + at}}`

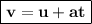
Substituting values of v, u & a in the equation:

`\sf \implies 30 = 10 + 2t`

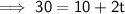
Substract 10 from both sides:

`\sf \implies 30 - 10 = (10 - 10) + 2t`

`\sf \implies 20 = 2t`

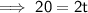
20 = 2t is equivalent to 2t = 20:

`\sf \implies 2t = 20`

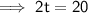
Dividing both sides by 2:

`\sf \implies \frac{ \cancel{2}t}{ \cancel{2}} = (20)/(2)`

`\sf \implies t = \frac{10 * \cancel{2}}{ \cancel{2}}`

`\sf \implies t = 10 \: s`

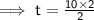
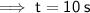
So,

Time taken (t) by bike to increase its velocity from 10 m/s to 30 m/s with an acceleration of 2 m/s² = 10 seconds